A associação de resistores em série é o tipo de associação em que os resistores estão ligados no mesmo ramo do circuito elétrico. Por causa desse tipo de associação, a corrente elétrica que atravessa cada resistor tem o mesmo valor, enquanto a tensão elétrica é diferente para cada resistor.
Leia também: Afinal, o que é uma associação de resistores?
Tópicos deste artigo
- 1 - Resumo sobre a associação de resistores em série
- 2 - Videoaula sobre a associação de resistores em série
- 3 - O que é associação de resistores em série?
- 4 - Como funciona a associação de resistores em série?
- 5 - Fórmulas da associação de resistores em série
- 6 - Como calcular associação de resistores em série?
- 7 - Associação de resistores mista
- 8 - Exercícios resolvidos sobre associação de resistores em série
Resumo sobre a associação de resistores em série
- A associação de resistores em série é o tipo de associação em que os resistores são associados sequencialmente.
- Para que a associação dos resistores em série funcione, é necessário conectar o circuito elétrico a uma tensão elétrica.
- Na associação dos resistores em série, é possível calcular a resistência elétrica equivalente dos resistores.
- Na associação de resistores em série, a corrente elétrica que passa em cada resistor tem o mesmo valor, enquanto a tensão elétrica é diferente em todos os resistores.
- A associação de resistores mista é aquela em que os resistores são associados paralela e sequencialmente.
Videoaula sobre a associação de resistores em série
O que é associação de resistores em série?
A associação de resistores em série é realizada por meio da conexão de dois ou mais resistores no mesmo ramo em um circuito elétrico. Essa associação é escolhida sempre que se deseja aumentar a resistência elétrica total ou a tensão elétrica do circuito elétrico. Abaixo, temos uma representação de como é a associação dos resistores em série.

Existem algumas propriedades da associação de resistores em série:
- Resistência elétrica: na associação de resistores em série, a resistência elétrica equivalente tem valor maior para as mesmas resistências elétricas na associação de resistores em paralelo.
- Corrente elétrica: na associação de resistores em série, a corrente elétrica que passa em cada resistor tem o mesmo valor.
- Tensão elétrica: na associação de resistores em série, a tensão elétrica tem diferentes valores em todos os resistores, a menos que os resistores tenham a mesma resistência elétrica.
Como funciona a associação de resistores em série?
A associação dos resistores em série funciona quando conectamos dois ou mais resistores em série em um circuito elétrico e, em seguida, o ligamos a uma tensão elétrica (diferença de potencial elétrico — ddp), fazendo com que as cargas elétricas se movimentem e a corrente elétrica atravesse todo o circuito elétrico.
Fórmulas da associação de resistores em série
→ Fórmula geral da associação de resistores em série
\(R_{eq}=R_1+R_2…R_N\)
- Req → resistência elétrica equivalente, medida em Ohm [Ω].
- R1 → resistência do primeiro resistor, medida em Ohm [Ω].
- R2 → resistência do segundo resistor, medida em Ohm [Ω].
- RN → resistência do énesimo resistor, medida em Ohm [Ω].
→ Primeira lei de Ohm
\(U=R \cdot i\)
- U → diferença de potencial elétrico ou tensão elétrica, medida em Volt [V].
- R → resistência elétrica, medida em Ohm [Ω].
- i → corrente elétrica, medida em Ampère [A].
Como calcular associação de resistores em série?
Na associação dos resistores em série, calculamos a resistência elétrica equivalente dos seus resistores empregando a sua fórmula. Pensando nisso, selecionamos um exemplo abaixo:
- Exemplo:
Um circuito tem três resistores ligados em série, com valores iguais a 2 Ω, 4 Ω e 6 Ω. Sabendo que eles são percorridos por uma corrente elétrica de 10 A, calcule a tensão elétrica associada nesse circuito elétrico:
Resolução:
Primeiramente, calcularemos a resistência elétrica equivalente dos resistores associados em série usando a sua fórmula:
\(R_{eq}=R_1+R_2+R_3\)
\(R_{eq}=2+4+6\)
\(R_{eq}=12 Ω\)
Por fim, calcularemos a tensão elétrica usando a fórmula da primeira lei de Ohm:
\(U=R \cdot i\)
\(U=12 \cdot 10\)
\(U=120 V\)
Associação de resistores mista
A associação de resistores mista é realizada por meio da conexão de três ou mais resistores em série e em paralelo em um circuito elétrico. Essa associação é escolhida sempre para circuitos elétricos complexos e quando se deseja obter valores flexíveis de corrente elétrica, tensão elétrica e resistência elétrica equivalente, que seriam difíceis de se conseguir fazendo apenas uma associação de resistores em série ou em paralelo. Abaixo temos uma representação de como é a associação dos resistores mista.
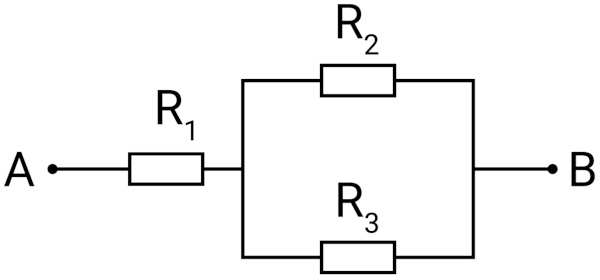
Acesse também: O que é a associação de resistores em paralelo?
Exercícios resolvidos sobre associação de resistores em série
Questão 1
(Fatec) Dois resistores, de resistências R0 = 5,0 Ω e R1 = 10,0 Ω são associados em série, fazendo parte de um circuito elétrico. A tensão V0 medida nos terminais de R0 é igual a 100V. Nessas condições, a corrente que passa por R1 e a tensão nos seus terminais são, respectivamente:
A) 5 ∙ 10-2 A; 50 V.
B) 1,0 A; 100 V.
C) 20 A; 200 V.
D) 30 A; 200 V.
E) 15 A; 100 V.
Resolução:
Alternativa C.
Primeiramente, calcularemos a corrente elétrica que percorre o resistor R0 empregando a fórmula da primeira lei de Ohm:
\(U=R \cdot i\)
\(100=5 \cdot i\)
\(i= \frac {100}{5}\)
\(i=20 A\)
Por fim, calcularemos a tensão elétrica nos terminais do resistor R1 empregando a fórmula da primeira lei de Ohm:
\(U=R \cdot i\)
\(U=10 \cdot 20\)
\(U=200 V\)
Questão 2
(UEL) Considere os valores indicados no esquema a seguir que representa uma associação de resistores.

O resistor equivalente dessa associação, em ohms, vale:
A) 8
B) 14
C) 20
D) 32
E) 50
Resolução:
Alternativa E.
Primeiramente, calcularemos a resistência elétrica em cada resistor empregando a fórmula da primeira lei de Ohm. Então, no resistor 1, temos:
\(U_1=R_1 \cdot i\)
\(7,0=R_1 \cdot 0,40\)
\(R_1= \frac {7,0}{0,40}\)
\(R_1=17,5 Ω\)
No resistor 2, temos:
\(U_2=R_2 \cdot i\)
\(5,0=R_2 \cdot 0,40\)
\(R_2= \frac {5,0}{0,40}\)
\(R_2=12,5 Ω\)
No resistor 3, temos:
\(U_3=R_3 \cdot i\)
\(8,0=R_3 \cdot 0,40\)
\(R_3= \frac {8,0}{0,40}\)
\(R_3=20 Ω\)
Por fim, calcularemos a resistência equivalente da associação em série empregando a sua fórmula:
\(R_{eq}=R_1+R_2+R_3\)
\(R_{eq}=17,5+12,5+20\)
\(R_{eq}=50 Ω\)
Fontes
NUSSENZVEIG, Herch Moysés. Curso de física básica: Eletromagnetismo (vol. 3). Editora Blucher, 2015.
HALLIDAY, David; RESNICK, Robert; WALKER, Jearl. Fundamentos da Física: Eletromagnetismo (vol. 3). 10. ed. Rio de Janeiro, RJ: LTC, 2016.
SAMPAIO, José Luiz; CALÇADA, Caio Sérgio. Universo da Física: Ondulatória. Eletromagnetismo. Física Moderna. São Paulo: Atual, 2005.




